The Synthetic Control Method
2025-11-11
Introduction to Synthetic Control Methods (SCM)
Historical roots
Originates from the comparative case study framework:
- Small number of treated units.
- Compare treated units against untreated units to infer causal effects.
- Small number of treated units.
Connection to Difference-in-Differences (DiD)
DiD assumes potential outcomes for unit \(j\) at time \(t\) under no treatment follow:
\[ y_{jt}(0) = \mu_j + \lambda_t + \epsilon_{jt}, \]
where \(\mu_j\) is a unit-specific intercept (unobserved) and \(\lambda_t\) is a time-specific effect common to all units.
The errors \(\epsilon_{jt}\) capture idiosyncratic shocks.SCM generalizes this to an interactive fixed effects model, allowing time factors to affect units differently:
\[ y_{jt}(0) = \mathbf{\mu}_j^\top \mathbf{\lambda}_t + \epsilon_{jt}, \]
where \(\mathbf{\mu}_j \in \mathbb{R}^r\) and \(\mathbf{\lambda}_t \in \mathbb{R}^r\) are latent factor vectors.
- Each dimension \(k = 1,\dots,r\) represents a latent factor driving variation across units and time.
- SCM attempts to construct a weighted combination of control units that approximates \(\mathbf{\mu}_j^\top \mathbf{\lambda}_t\) for the treated unit.
- Each dimension \(k = 1,\dots,r\) represents a latent factor driving variation across units and time.
What Is An Average?
We need to understand what an average is.
The arithmetic mean of a finite sequence of real numbers, \((x_1, x_2, \dots, x_n) \in \mathbb{R}^n\), is defined as a weighted sum
\[ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i = \frac{x_1 + x_2 + \cdots + x_n}{n}. \]
using \(\dfrac{1}{n}\) as the weight where \(n\) is the number of elements in the sequence.
- For example, say you have 12 apples and your friend has 18. Denote this as the sequence \(A = (12, 18) \in \mathbb{N}^2\). There are two elements in this sequence, meaning our weight is \(dfrac{1}{2}\). Thus, the mean is
\[ \bar{x} = \frac{1}{2}(12 + 18)=((0.5. \times 12) + (0.5 \times 18))=6+9 = 15. \]
On average, you have 15 apples. Pretty straightforward.
- We can also represent the same example as a row vector:
\[ \mathbf{x} = \begin{bmatrix} 12 & 18 \end{bmatrix} \in \mathbb{R}^{1 \times 2}. \]
Here, the sequence \(A\) is mapped onto a row vector. Think of this as the first row of a spreadsheet, where each column entry represents a person. The value in each column is the number of apples that person has.
To compute the average, we apply the same formula. Since there are two people, the weight we use for the sum is \(1/2\). Thus,
\[ \mathbf{x}^\top \left(\tfrac{1}{2}\mathbf{1}_2\right) = \begin{bmatrix} 12 & 18 \end{bmatrix} \cdot \left(\tfrac{1}{2} \begin{bmatrix} 1 \\ 1 \end{bmatrix}\right) = \begin{bmatrix} 12 \times 0.5 & 18 \times 0.5 \end{bmatrix} = \begin{bmatrix} 6 & 9 \end{bmatrix}, \]
and then summing entries:
\[ \mathbf{1}_2^\top \begin{bmatrix} 6 \\ 9 \end{bmatrix} = 6 + 9 = 15. \]
This is mathematically equivalent to dividing the sum of the entries by 2, as we did with scalars.
In other words, arithmetic averaging is just taking a weighted sum, where each weight is the reciprocal of the number of entries.
- Let’s extend the idea of averaging to multiple time periods. Suppose today you have 12 apples and tomorrow 30, while your friend has 18 today and 22 tomorrow. We can put this into a matrix, or a collection of vectors, where each row is a time period and each column is a person:
\[ \mathbf{Y} = \begin{bmatrix} 12 & 18 \\ 30 & 22 \end{bmatrix} \in \mathbb{R}^{2 \times 2}. \]
Now, we have columns and rows. Each row represents a snapshot in time, and each column represents a person.
To find the average number of apples per time period, we use the same weights as before (1/2 for each person). Multiplying the matrix by the weight vector gives a row-wise weighted sum:
\[ \mathbf{w} = \begin{bmatrix} 1/2 \\ 1/2 \end{bmatrix}, \quad \bar{\mathbf{x}} = \mathbf{Y} \mathbf{w} = \begin{bmatrix} 12 & 18 \\ 30 & 22 \end{bmatrix} \begin{bmatrix} 1/2 \\ 1/2 \end{bmatrix} = \begin{bmatrix} 15 \\ 26 \end{bmatrix}. \]
Interpretation: Today, the average is 15 apples; tomorrow, the average is 26 apples.
Row-wise averaging is thus just taking a weighted sum across the columns for each row.
Each row “collapses” into a single number representing the average for that time period.This concept generalizes to any time-series or panel data, such as GDPs, incomes, or other outcomes measured across multiple units.
What Are We Weighting For? Introducing Weighted Averages
You are at a bar with your friend. You earn $60k/year. Your friend earns $70k/year. The simple average of your incomes is:
\[ \mathbf{x} = \begin{bmatrix} 60000 & 70000 \end{bmatrix}, \quad \mathbf{w} = \begin{bmatrix} \frac{1}{2} \\[1mm] \frac{1}{2} \end{bmatrix}, \] and the average is computed like \[ \bar{x} = \mathbf{x} \mathbf{w} = \begin{bmatrix} 60000 & 70000 \end{bmatrix} \begin{bmatrix} \frac{1}{2} \\[1mm] \frac{1}{2} \end{bmatrix} = \frac{1}{2}\cdot 60000 + \frac{1}{2}\cdot 70000 = 65000 \text{/year}. \]
Now, suddenly Bill Gates walks in, with a net income of $107B/year. Taking the simple average of all three income levels, we now just add one to the denominator since we now have three people:
\[ \mathbf{x} = \begin{bmatrix} 60000 & 70000 & 1.07\times 10^{11} \end{bmatrix}, \quad \mathbf{w} = \begin{bmatrix} \frac{1}{3} \\[1mm] \frac{1}{3} \\[1mm] \frac{1}{3} \end{bmatrix} \]
\[ \bar{x} = \mathbf{x} \mathbf{w} = \frac{1}{3}\cdot 60000 + \frac{1}{3}\cdot 70000 + \frac{1}{3}\cdot 1.07\times 10^{11} \approx 35.7 \text{ B/year}. \]
Clearly, treating Bill Gates the same as the others skews the average. In other words, if the bartender next day bragged about earning 50k that night, we’d say: “It’s not that you earned 50k organically; a wealthy dude happened to be there that night, that is not a typical night for you.
We would not say that this is business as usual, we’d say that times where Bill Gates comes in are anomalous and cannot be used as the baseline.
In other words, if we want a meaningful “bar average,” Bill should likely get much less weight (if any) than the other patrons.
There is no law of nature that says the weight must be \(1/n\). Practically, we can assign weights however we like.
Instead of treating Bill as equal to you two, we can give each person a weight \(w_i \in [0,1]\), deciding how much they count in the average.
Previously, in the arithmetic mean, \(w_i = 1/n\).Formally, the weighted average is:
\[ \bar{x}_{\text{weighted}} = \sum_{i=1}^{n} w_i x_i, \quad \sum_{i=1}^{n} w_i = 1. \]
Here, Bill can get a tiny weight (if any), and you and your friend get larger weights, giving a more reasonable “average bar income.”
Suppose we only care about you and your friend, and ignore Bill Gates (weight = 0):
\[ \mathbf{x} = \begin{bmatrix} 60000 & 70000 & 1.07\times 10^{11} \end{bmatrix}, \quad \mathbf{w} = \begin{bmatrix} 0.5 \\[1mm] 0.5 \\[1mm] 0 \end{bmatrix}. \]
Then the weighted average is:
\[ \bar{x} = \mathbf{x} \mathbf{w} = 0.5\cdot 60000 + 0.5\cdot 70000 + 0\cdot 1.07\times 10^{11} = 65000 \,\text{/year}. \]
So the average is back to what it was initially. Bill clearly is not representative of the bar (or even the country).
Giving him as much weight as regular patrons does not make sense. Weighted averages let us reflect this reality.
Applied Averages
In real life, weights are never handed down from the heavens: we, the econometricians, must assign them. Assigning them poorly can produce nonsensical averages if we wish to use averages as comparisons, as we often do.
The arithmetic average is familiar to applied economists, coming up sometimes as the national average. It is used all the time in policy discussions, for example:
But again, this assumes that the aggregate weights produce a meaningful comparison for a single unit — which may not be true (recall the Bill Gates example).
Suppose we have one unit exposed to terrorism in 1975 (the Basque Country), and a set of 16 other units that are not exposed. We want to estimate the effect of terrorism on GDP per capita. How to choose the weights?
The Basque Country is much wealthier than many areas of Spain, has a unique political climate, and was more educated and industrialized than other areas.
Optimization can solve this problem. Instead of us just arbitrarily assigning weights, we choose the weights that minimize the pre-intervention gap between the Basque Country and the weighted donor units.
Using Least Squares
We could use ordinary least-squares, where the coefficient vector returned to us will be the weights for our control units.
We index time by \(t \in \mathbb{N}\) and units by \(j \in \mathbb{N}\), where unit 1 is treated and the others are controls.
- \(\mathcal{T}_1 = \{1,\dots,T_0\} \subset \mathbb{N}\): set of pre-treatment periods, with cardinality \(|\mathcal{T}_1| = T_0\)
- \(\mathcal{T}_2 = \{T_0+1,\dots,T\} \subset \mathbb{N}\): set of post-treatment periods, with cardinality \(|\mathcal{T}_2| = T - T_0\)
- \(\mathcal{J} = \{1,\dots,J+1\} \subset \mathbb{N}\): set of all units (1 treated + \(J\) controls)
- \(\mathcal{J}_0 = \mathcal{J} \setminus \{1\} = \{2,\dots,J+1\} \subset \mathbb{N}\): set of untreated donor units, with cardinality \(|\mathcal{J}_0| = J\)
- \(\mathbf{y}_1 \in \mathbb{R}^{T}\): outcome vector (e.g., GDP per capita) for the treated unit over all \(T\) time periods
- \(\mathbf{Y}_0 \in \mathbb{R}^{T \times J}\): donor matrix; each column is a control unit, each row is a time period
- \(\mathbf{w} \in \mathbb{R}^{J}\): vector of donor weights where each entry \(w_j\) indicates the contribution of control unit \(j \in \mathcal{J}_0\) to the synthetic control
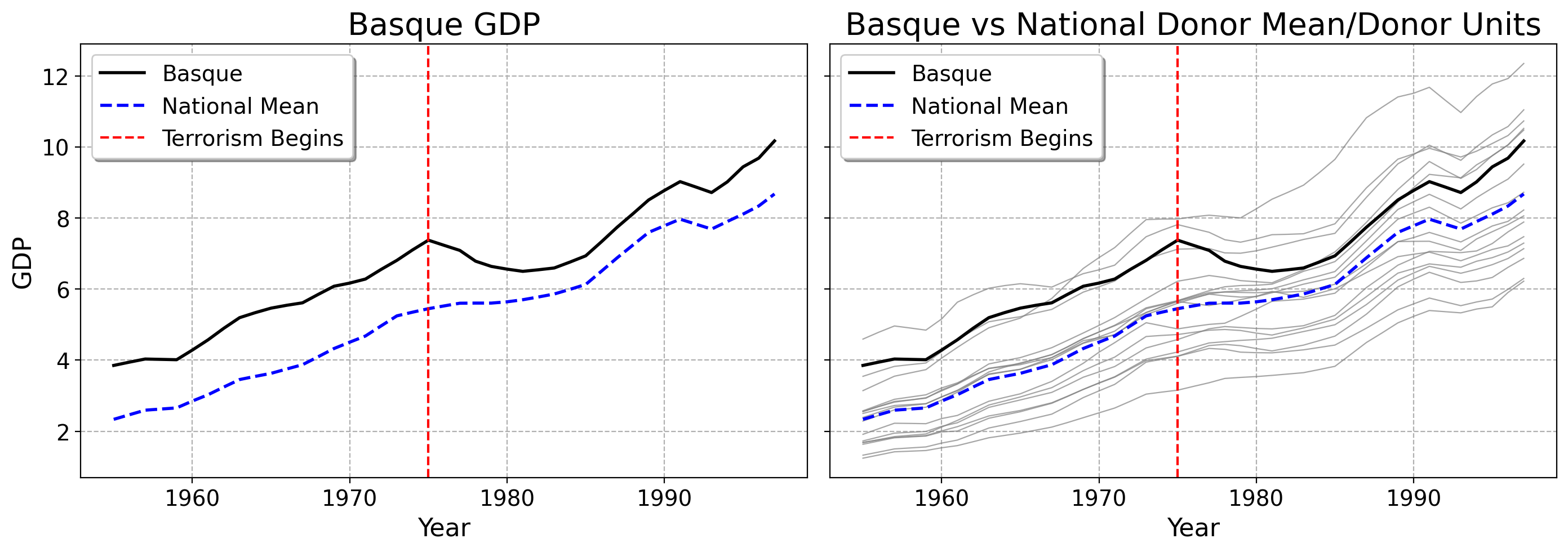
We can see the Basque column as well as some of the donor columns. We wish to take a weighted average of these control unit columns to approximate the Basque Country in the preintervention period. Given that there is good pretreatment fit between the weighted average and the Basque Country, the post-1975 predictions serve as the counterfactual estimate.
Reminder: a weighted average can be written as
\[ \hat{y}_{1t} = \mathbf{Y}_0 \mathbf{w} = \sum_{j \in \mathcal{J}_0} w_jy_{jt}, \qquad t \in \mathcal{T}_1 \cup \mathcal{T}_2. \]
| year | Andalucia | Aragon | Baleares (Islas) | Basque | Canarias | Cantabria | Castilla Y Leon | Castilla-La Mancha | Cataluna | Comunidad Valenciana |
|---|---|---|---|---|---|---|---|---|---|---|
| 1955 | 1.68873 | 2.28877 | 3.14396 | 3.85318 | 1.91438 | 2.55941 | 1.72915 | 1.32776 | 3.54663 | 2.57598 |
| 1956 | 1.7585 | 2.44516 | 3.34776 | 3.94566 | 2.07184 | 2.69387 | 1.83833 | 1.4151 | 3.69045 | 2.7385 |
| 1957 | 1.82762 | 2.6034 | 3.54963 | 4.03356 | 2.22608 | 2.82034 | 1.94766 | 1.50357 | 3.82683 | 2.89989 |
| 1958 | 1.85276 | 2.63903 | 3.64267 | 4.02342 | 2.22087 | 2.87903 | 1.97137 | 1.53142 | 3.87568 | 2.96351 |
| 1959 | 1.87803 | 2.67709 | 3.73486 | 4.01378 | 2.21344 | 2.94373 | 1.99514 | 1.55934 | 3.92174 | 3.02621 |
| 1960 | 2.01014 | 2.88146 | 4.05884 | 4.28592 | 2.35768 | 3.13703 | 2.13882 | 1.66752 | 4.24179 | 3.21929 |
| 1961 | 2.12918 | 3.09954 | 4.36025 | 4.57434 | 2.44573 | 3.32762 | 2.2395 | 1.75243 | 4.57534 | 3.36247 |
| 1962 | 2.28035 | 3.35918 | 4.64617 | 4.89896 | 2.64824 | 3.55534 | 2.45423 | 1.92045 | 4.83805 | 3.56998 |
| 1963 | 2.43102 | 3.61418 | 4.91153 | 5.19701 | 2.84476 | 3.77142 | 2.67224 | 2.0919 | 5.08133 | 3.76521 |
| 1964 | 2.50885 | 3.68009 | 5.0507 | 5.3389 | 2.95116 | 3.8394 | 2.77778 | 2.18259 | 5.1581 | 3.82369 |
- Choose weights to minimize the squared pre-intervention difference between Basque and the weighted donors:
\[ \mathbf{w}^{\ast} = \underset{\mathbf{w} \in \mathbb{R}^J}{\operatorname*{argmin}} \; \| \mathbf{y}_1 - \mathbf{Y}_0 \mathbf{w} \|_2^2, \qquad t \in \mathcal{T}_1 \]
- In practice, this is just OLS on the pre-1975 period, where \(\mathbf{y}_1\) is the Basque GDP column and \(\mathbf{Y}_0\) contains donor columns.
- The regression coefficients (betas, \(\beta\)) are the weights \(\mathbf{w}^{\ast}\).
- Multiply each control unit by its weight and sum across donors to get predicted Basque GDP pre- and post-intervention.
- Define the period-level treatment effect as the difference between observed outcome and synthetic control prediction:
\[ \hat{\tau}_{1t} = y_{1t} - \hat{y}_{1t}, \qquad t \in \mathcal{T}_2 \]
- Total treatment effect (TTE):
\[ \text{TTE} = \sum_{t \in \mathcal{T}_2} \hat{\tau}_{1t} = \sum_{t \in \mathcal{T}_2} \Big( y_{1t} - \hat{y}_{1t} \Big) \]
- Average treatment effect on the treated (ATT):
\[ \text{ATT} = \frac{1}{T_2} \sum_{t \in \mathcal{T}_2} \hat{\tau}_{1t} = T_2^{-1} \sum_{t \in \mathcal{T}_2} \Big( y_{1t} - \hat{y}_{1t} \Big) \]
- Percentage treatment effect (PTE) relative to the counterfactual mean:
\[ \%\text{Treatment Effect} = \frac{\frac{1}{T_2} \sum_{t \in \mathcal{T}_2} \hat{\tau}_{1t}} {\frac{1}{T_2} \sum_{t \in \mathcal{T}_2} \hat{y}_{1t}} \times 100 \]
Intuition:
- \(\hat{\tau}_{1t}\) shows the effect at each post-treatment time point.
- ATT summarizes the overall post-treatment deviation.
- TTE aggregates deviations into a single cumulative number.
- PTE scales ATT relative to the counterfactual, giving magnitude in context.
Least Squares Cont.
Here are the weights OLS returns to us for the 16 donor units:
| regionname | Weight |
|---|---|
| Andalucia | 4.17551 |
| Aragon | -1.50358 |
| Baleares (Islas) | -0.0107201 |
| Canarias | -0.0168126 |
| Cantabria | 0.261694 |
| Castilla Y Leon | 6.07601 |
| Castilla-La Mancha | -2.6561 |
| Cataluna | -0.945626 |
| Comunidad Valenciana | 0.860017 |
| Extremadura | -1.93895 |
| Galicia | -2.96441 |
| Madrid (Comunidad De) | 0.343366 |
| Murcia (Region de) | -0.620705 |
| Navarra (Comunidad Foral De) | 0.583705 |
| Principado De Asturias | 0.51578 |
| Rioja (La) | -0.94721 |
Notice that OLS assigns some positive and some negative weights. These tell us how similar the control units is to the treated unit. Notice how some units have negative weights. These can be hard to interpret substantively: which units are truly most similar to the Basque Country before terrorism happened? Is it Andalucia or Castilla Y Leon?
Here are some of the predicted donors plotted against the Basque Country
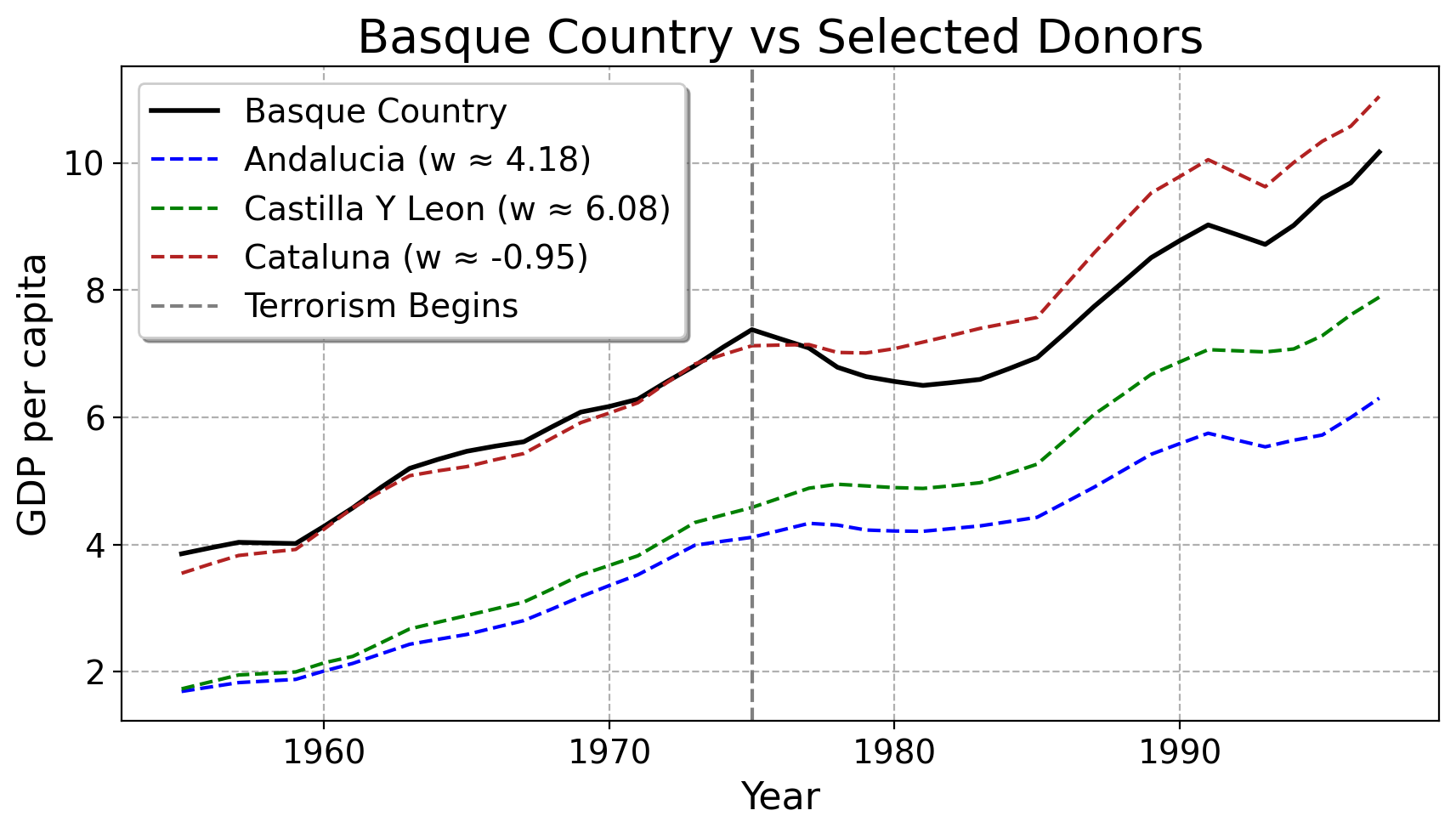
Much of this does not really square very nicely with intution. Cataluna, which is very close to the Basque Country (both literally in terms of GDP and being a French border region in Northern Spain) gets negative weight from OLS. The units which are much farther away from the Basque Country (on top of having much different political/economic histories) get much more weight
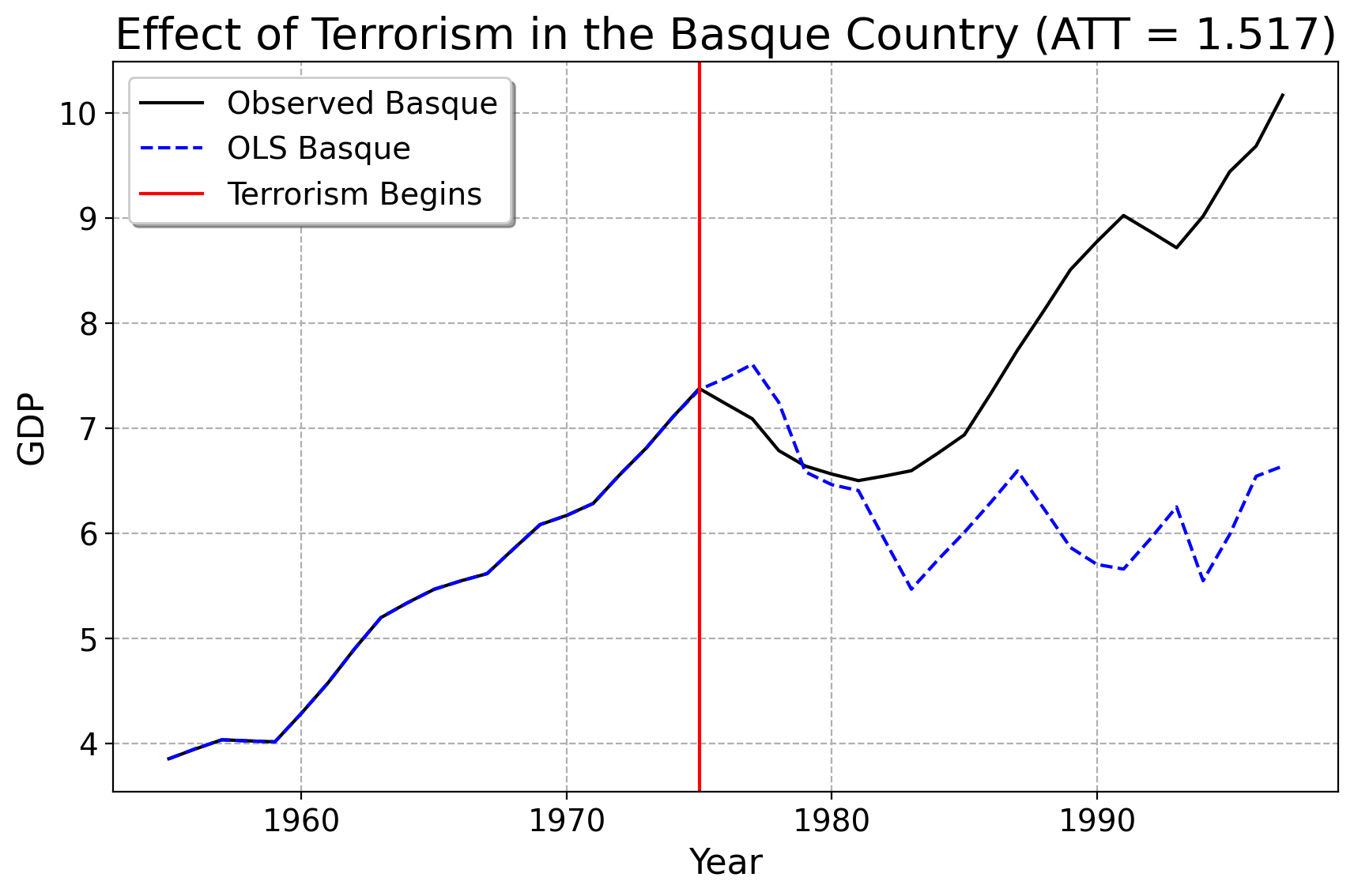
Here is our prediction using OLS. Unfortunately, while OLS fits very well to the Basque Country before terrorism happened, the out-of-sample/post-1975 predicions exhibits a lot more variance than any control unit in the pre-treatment period did. The counterfactual has a weird zig-zag-y prediction. We can see that the prediction line for the Basque country suggests that its economy would have fallen off a cliff, had terrorism not happened. In other words, if the OLS estmate is to be taken seriously, the onset of terrorism saved the Basque economy… This does not seem like a sensible finding historically, or a very reasonable prediction statistically.
How To Change The Weights
What if we could adjust the weights so the synthetic Basque stays within the range of the donor units?
In other words, we want the model predictions to lie inside the full range of the donors only.
The plot below shows the area spanned by all donor regions in Spain (shaded), along with the Basque Country. This visualizes the full feasible range for any weighted average of donors.
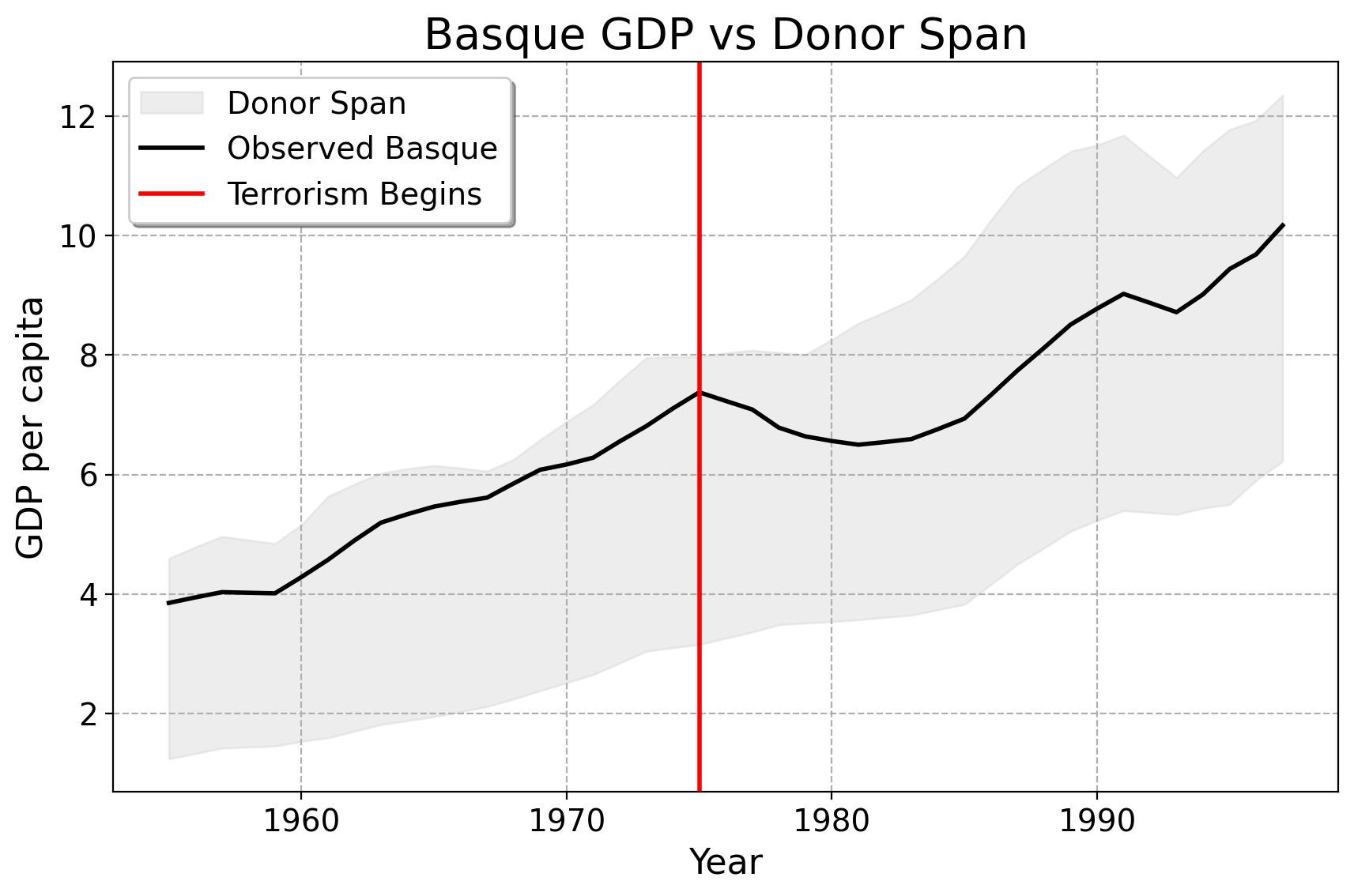
Classic Synthetic Control Model
The classic SCM estimator solves the following ordinary least-squares regression problem:
\[ \begin{aligned} \mathbf{w}^{\mathrm{SCM}} &= \underset{\mathbf{w}^{\mathrm{SCM}} \in \mathcal{W}_{\mathrm{conv}}}{\operatorname*{argmin}} \; \left\| \mathbf{y}_1 - \mathbf{Y}_0 \mathbf{w}^{\mathrm{SCM}} \right\|_2^2 \quad \forall \, t \in \mathcal{T}_{1}, \\ \mathcal{W}_{\mathrm{conv}} &= \left\{ \mathbf{w}^{\mathrm{SCM}} \in \mathbb{R}_{\ge 0}^{J} \;\middle|\; \mathbf{1}^\top \mathbf{w} = 1 \right\} \end{aligned} \]
We want to combine the donor regions to best match the treated unit before the intervention. By requiring all weights to be nonnegative and sum to 1, the synthetic Basque is a weighted average that stays inside the range of the donors—it can’t “overshoot” or assign negative importance to any region.
Given the optimal weights \(\mathbf{w}^{\mathrm{SCM}}\), the SCM prediction for the treated unit is
\[ \hat{\mathbf{y}}_1^{\mathrm{SCM}} = \mathbf{Y}_0 \mathbf{w}^{\mathrm{SCM}}\equiv\sum_{j \in \mathcal{J}_0} w_j^{\mathrm{SCM}} \, y_{jt}, \quad \forall \, t \in \mathcal{T} \] —
SCM for Basque
- Here is the result of the regression model. The Basque Country is best reproduced by 85% Catalonia and 15% Madrid.
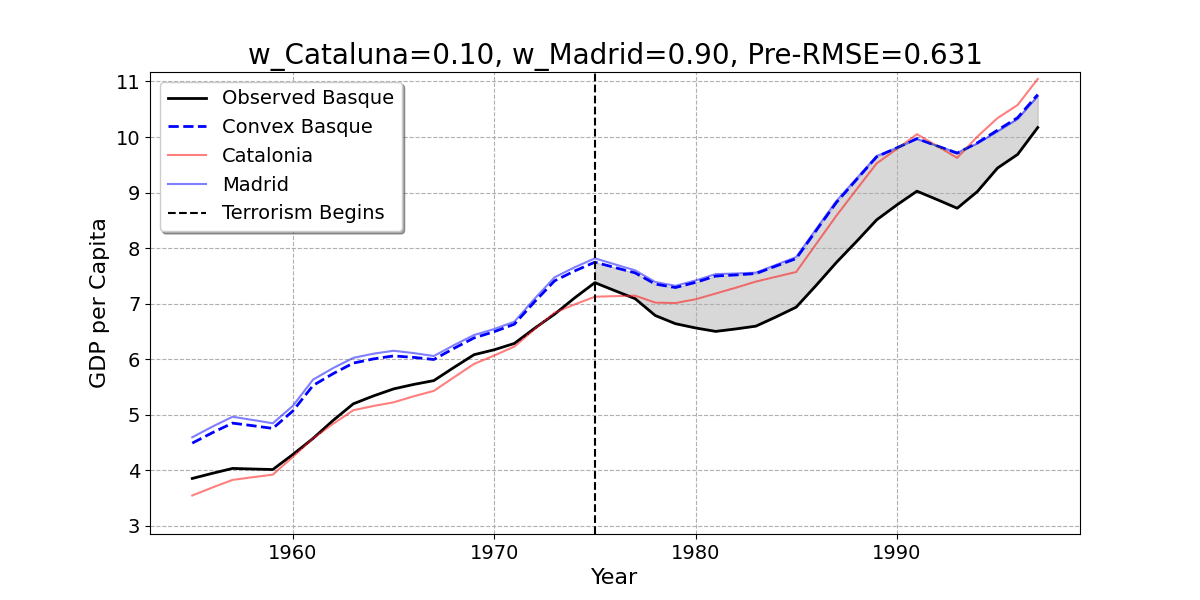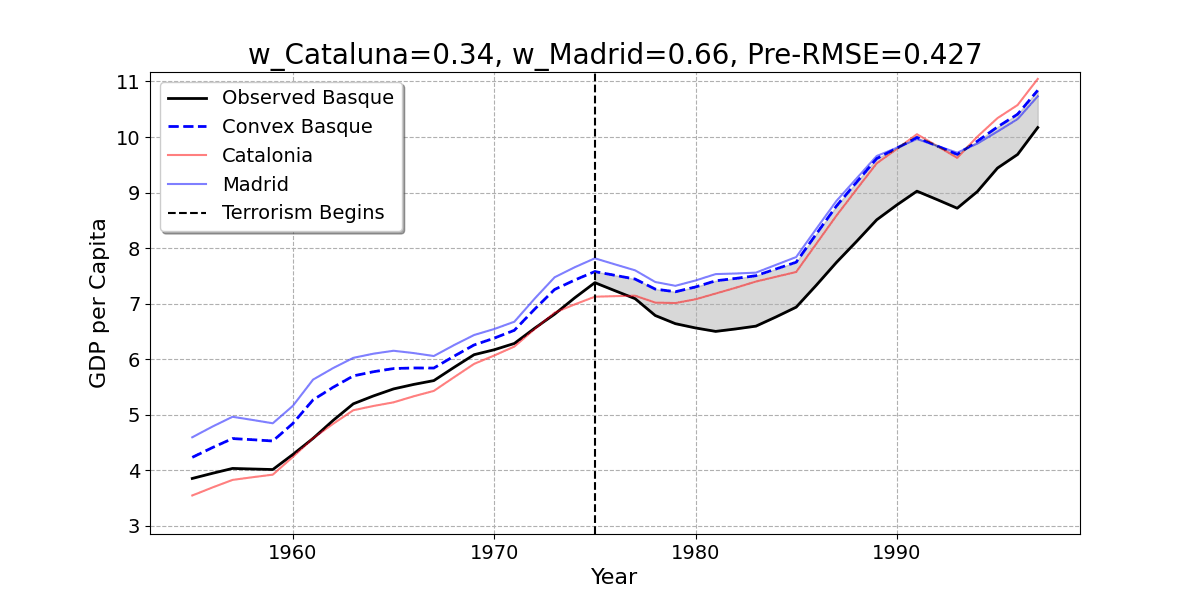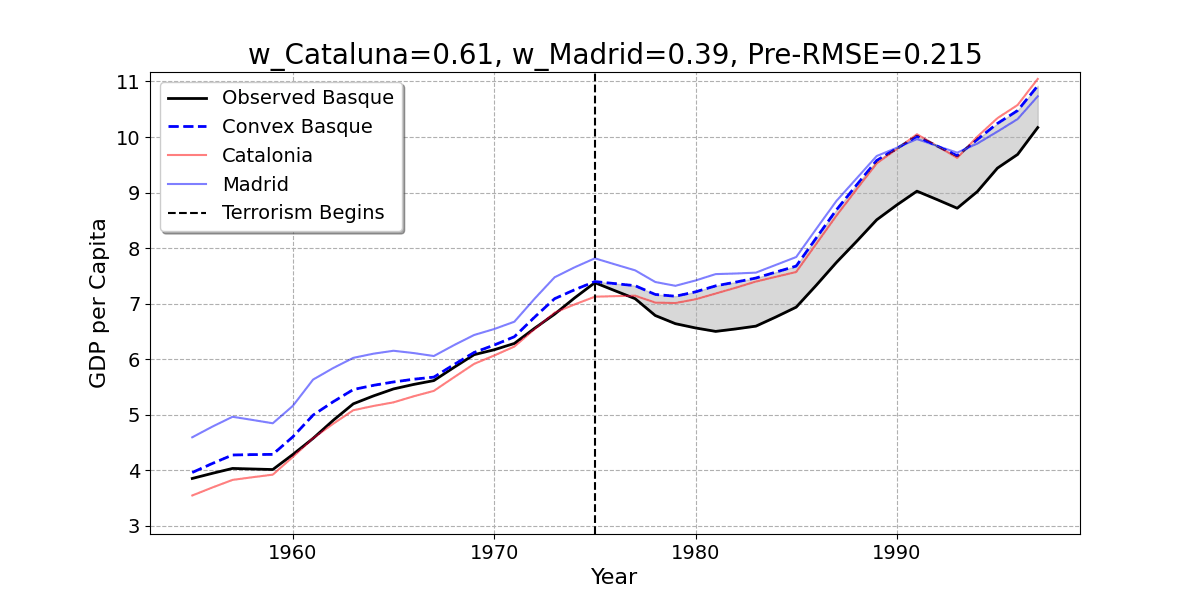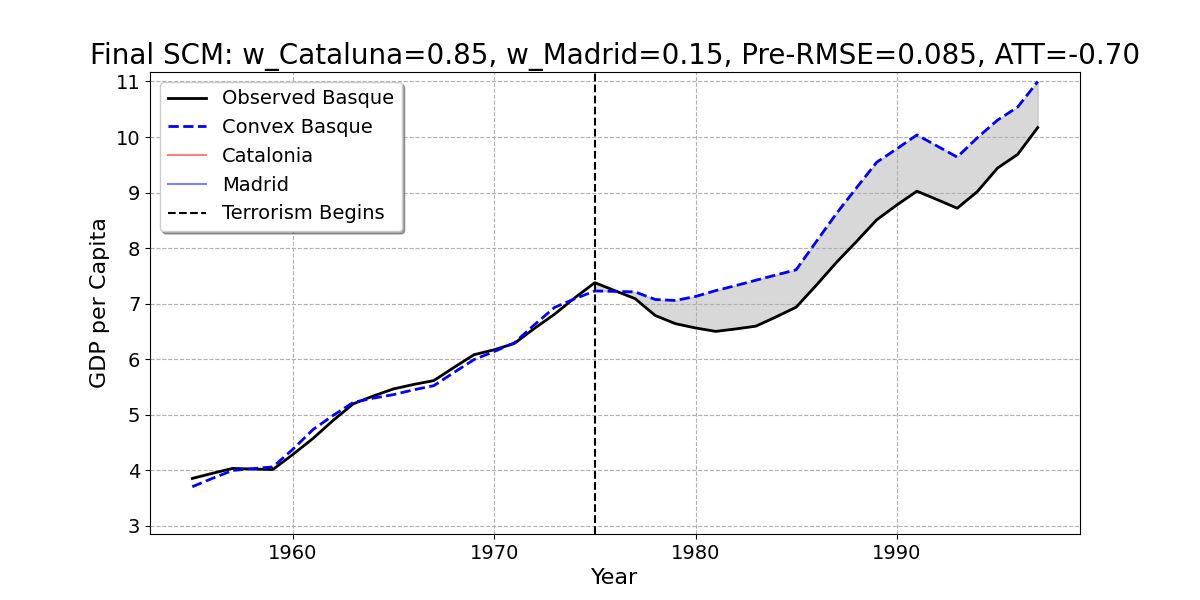
Convex Combination
Inference: Placebos
Validating SCM designs are important as well, Consider a few robustness checks:
ideally, shifting the treatement back in time should not change the practical results of the conclusions very much.
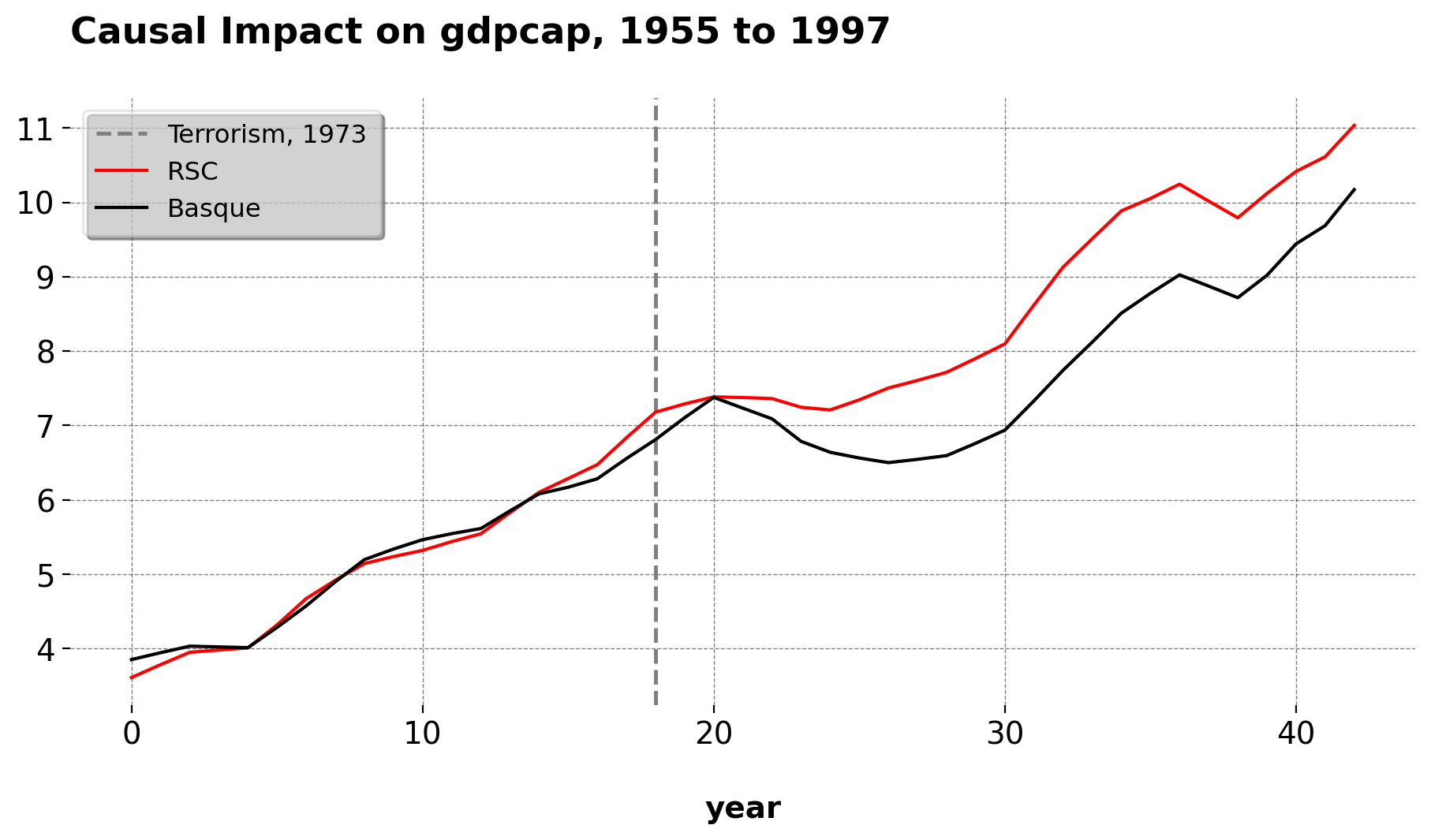
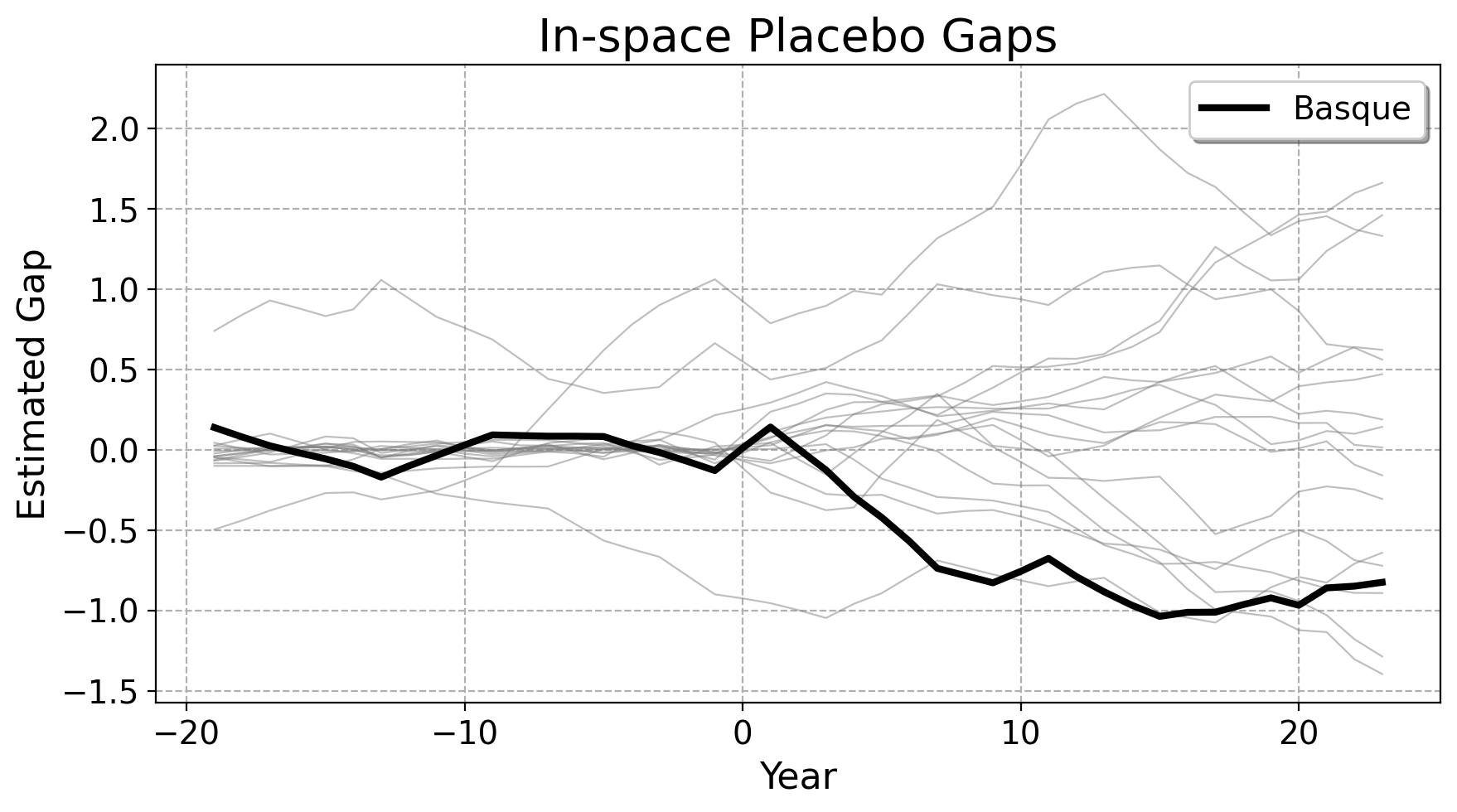
ideally, the treated unit’s treatment effect should look extreme compared to the placebo effect given to other untreated units. Here, we rerun the SCM over the other donor units.
Block Permutation Inference
A more modern approach however is block permutation. Block permutation accounts for temporal dependence in pre-treatment residuals.
- Residuals and Block Permutation Test
- Block Size
- Observed Test Statistic
- Permutation Test
- P-Values
- Confidence Intervals via Pre-Treatment Residuals
Pre-treatment residuals: difference between actual and synthetic control outcomes: \[ e_t = y_{1t} - \hat{y}_{1t}, \quad t \in \mathcal{T}_1 \]
Post-treatment treatment effects: difference after treatment: \[ \hat{\tau}_{1t} = y_{1t} - \hat{y}_{1t}, \quad t \in \mathcal{T}_2 \]
Goal: test if post-treatment gaps (the treatment effect) are unusually large relative to pre-treatment residuals (pre-treatment error). The problem is that we have small samples, so we need to use small sample inference.
Residuals may be very reasonably be correlated over time; we split pre-treatment residuals into blocks of length \(B\).
Compute lag-\(k\) autocorrelation:
\[ \text{ACF}(k) = \frac{\sum_{t=1}^{T_0-k} (e_t - \bar{e})(e_{t+k}-\bar{e})}{\sum_{t=1}^{T_0} (e_t-\bar{e})^2} \]
Choose \(B\) as the smallest lag where \(|\text{ACF}(B)| < c\), where \(c\) is some positive constant
Split residuals into \(N_B\) blocks:
\[ N_B = \left\lfloor \frac{T_0}{B} \right\rfloor, \quad \mathbf{e}^{(b)} = \{ e_{(b-1)B+1}, \dots, e_{bB} \}, \quad b=1,\dots,N_B \]
\[ S_{\text{obs}} = \frac{1}{T_2} \sum_{t \in \mathcal{T}_2} |\hat{\tau}_{1t}| \]
- Average absolute post-treatment effect.
- We now randomly resample pre-treatment blocks with replacement to create synthetic post-treatment residuals \(\mathbf{e}^{\ast(m)}\), \(m=1,\dots,M\):
\[ S^{\ast(m)} = \frac{1}{T_2} \sum_{t \in \mathcal{T}_2} \big| \mathbf{e}^{\ast(m)}_t \big| \]
- This generates a null distribution under no treatment.
- Global p-value:
\[ p_{\text{global}} = \frac{1}{M} \sum_{m=1}^{M} \mathbf{1}\big(S^{\ast(m)} \ge S_{\text{obs}}\big) \]
- Per-period p-values:
\[ p_t = \frac{1}{T_0} \sum_{s \in \mathcal{T}_1} \mathbf{1}\big(|e_s| \ge |\hat{\tau}_{1t}|\big), \quad t \in \mathcal{T}_2 \]
These are simply p-values measuring how unusual the absolute value of the ATT or a given post-intervnetion residual is relative to what we would expect.
- We define the \((1-\alpha)\) quantile of the absolute pre-treatment residuals using the infimum:
\[ q_{1-\alpha} \;=\; \inf \Bigg\{ q \in \mathbb{R} \;\Bigg|\; \frac{1}{T_0} \sum_{t \in \mathcal{T}_1} \mathbf{1} \Bigg( \Big|\, y_{1t} - \sum_{j \in \mathcal{J}_0} w_j \, y_{jt} \,\Big| \le q \Bigg) \ge 1 - \alpha \Bigg\}. \]
Definition / intuition:
The quantile \(q_{1-\alpha}\) is the smallest number such that at least \((1-\alpha)\) fraction of the pre-treatment residuals are less than or equal to it.
In other words, it tells us what magnitude of residuals is “typical” in the pre-treatment period.
Using this, we construct post-treatment confidence intervals around the estimated treatment effect:
\[ \mathrm{CI}_t = \Bigg[y_{1t} - \sum_{j \in \mathcal{J}_0} w_jy_{jt} - q_{1-\alpha},y_{1t} - \sum_{j \in \mathcal{J}_0} w_jy_{jt} + q_{1-\alpha} \,\Bigg]. \]
Interpretation:
If the post-treatment effect \(\hat{\tau}_{1t}\) lies outside this interval… it is larger than what we would normally expect based on pre-treatment variability.
This provides a simple, non-parametric confidence interval that accounts for the observed variation before treatment.
In theory, we could do this with moving blocks too, but that requires a little more bookeeping.
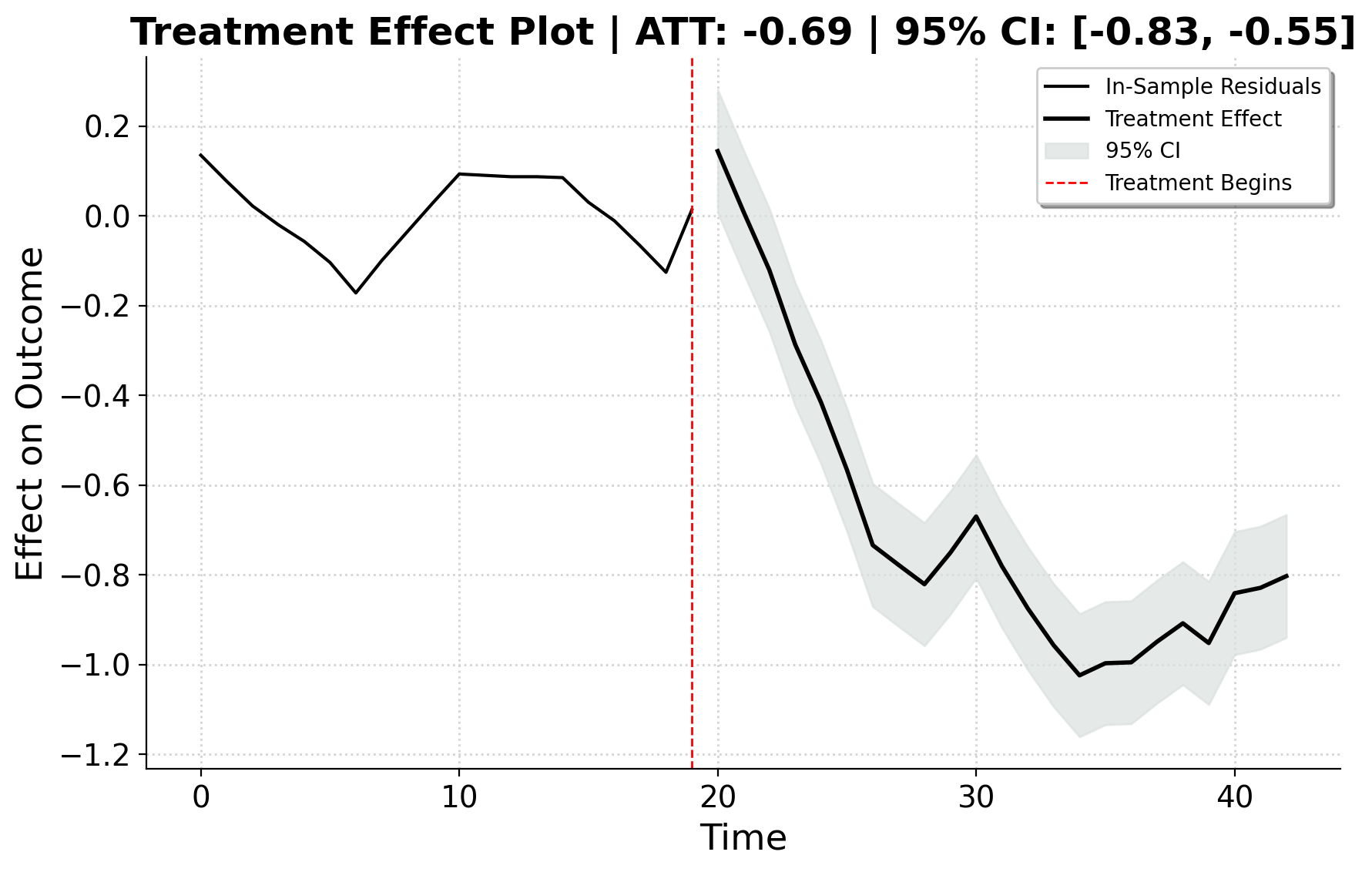
Block Results
Here are our results.
Key Takeaways for Classic SCM
Low-volatility series
Synthetic controls work best with aggregate, relatively smooth series.
Condition (informal): the pre-treatment volatility should be small relative to the signal, e.g. \[ \frac{\operatorname{sd}(y_{1t \in \mathcal{T}_{1}})}{\overline{y}_{1t \in \mathcal{T}_{1}}} \quad\text{is small.} \]Extended pre-intervention period
A long pre-treatment window improves identification.
Condition: the number of pre-periods \(T_0\) should be sufficiently large: \[ T_0 \gg r \quad\text{(where $r$ is the effective number of latent factors).} \]Small, relevant donor pool
More donors can increase interpolation bias and overfitting. Prefer a smaller donor set.
Condition (selection): restrict donor count \(J\) relative to pre-period information, e.g. \[ J \lesssim c \cdot T_0 \quad\text{for some modest constant } c, \]Sparsity aids interpretability
Fewer nonzero weights make the synthetic control easier to interpret.
Condition: prefer weight vectors \(\mathbf{w}\) with small support: \[ \|\mathbf{w}\|_0 << J \quad\text{or use the } \ell_1 \text{ norm: } \|\mathbf{w}\|_1 \]Plot your treated unit versus the donors (seriously)
Visual diagnostics: check level/trend alignment and extreme donors before fitting.
Diagnostic: inspect \(\{y_{jt}\}_{j\in \mathcal{J}_{0}}\) vs. \(y_{1t}\) for \(t \in \mathcal{T}_{1}\).Good pre-treatment fit matters
If pre-fit error is large, post-treatment inferences are unreliable.
Condition (quantitative): require a low pre-fit RMSE: \[ \text{RMSE}_{t \in \mathcal{T}_{1}} = \sqrt{\frac{1}{T_0}\sum_{t \in \mathcal{T}_{1}}\big(y_{1t}-\hat y_{1t}\big)^2} \]Out-of-sample validation is essential
Use placebo tests (in-time and in-space) to check robustness.
Condition (placebo): the treated unit’s post-treatment gap should be an outlier relative to the placebo distribution. If \(\widehat{\text{ATT}}_1\) is the treated ATT and \(\{\widehat{\text{ATT}}_j\}_{j\neq 1}\) are placebo ATTs, \[ p\text{-value} \approx \frac{1}{J}\sum_{j\neq 1} \mathbf{1}\big(|\widehat{\text{ATT}}_j|\ge |\widehat{\text{ATT}}_1|\big) \] should be small. Furthermore, the ATT for the real treatment period should not change substantively given reasonable in-time placebos.
Extensions
Synthetic Control methods have undergone many advances since their inception. If you wish to use Python to estimate synthetic controls, I wrote the largest such package that exists. See here for details:
